Disclaimer: The following is for informational purposes only and not financial advice. Always do your own due diligence. I am not a licensed advisor.

Understanding the Dividend Discount Model Formula: A Simple Guide to Stock Valuation

The Dividend Discount Model (DDM) is a widely used method for estimating the value of a company’s stock based on its expected future dividends. Whether you’re an investor looking to evaluate a dividend-paying stock or simply curious about how to calculate intrinsic stock value, understanding the DDM formula is essential.

In this article, we’ll dive into the various forms of the Dividend Discount Model, explore its components, and walk you through how to use this model to calculate the intrinsic value of a stock.

What is the Dividend Discount Model?

The Dividend Discount Model (DDM) is based on the principle that the value of a stock today is equal to the present value of its future dividends. Since money today is worth more than money in the future (thanks to the time value of money), the DDM calculates the intrinsic value of a stock by discounting future dividend payments.

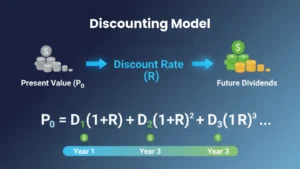
The basic formula for DDM is as follows:

P0=D11+R+D2(1+R)2+D3(1+R)3+⋯+D∞(1+R)∞P_0 = \frac{D_1}{1 + R} + \frac{D_2}{(1 + R)^2} + \frac{D_3}{(1 + R)^3} + \cdots + \frac{D_{\infty}}{(1 + R)^{\infty}}

Where:

P₀ is the current price (or intrinsic value) of the stock.
D₁, D₂, D₃, … are the dividends expected at the end of each year.
R is the required rate of return or discount rate.

The formula helps us calculate the present value of each future dividend, considering that the further into the future the dividend payment is, the less it is worth today.

The Basic Concept: Discounting Dividends

At its core, the Dividend Discount Model discounts future dividends by a specific rate (R), which is the rate an investor expects to earn from the stock. The formula accounts for an infinite number of future dividends since a company is assumed to be a going concern, living indefinitely unless it shuts down.

However, in practice, it’s not realistic to forecast an infinite stream of dividends, especially when an investor has a specific holding period in mind. This is where the modified Dividend Discount Model (DDM) comes into play.

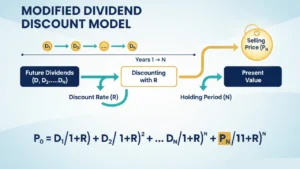
Modified Dividend Discount Model

The modified DDM assumes that a stock will be sold after a certain holding period, making the dividend stream finite. This version of the formula looks like this:

P0=D11+R+D2(1+R)2+⋯+DN(1+R)N+PN(1+R)NP_0 = \frac{D_1}{1 + R} + \frac{D_2}{(1 + R)^2} + \cdots + \frac{D_N}{(1 + R)^N} + \frac{P_N}{(1 + R)^N}

Where:

D₁, D₂, … Dₙ are the dividends paid during the holding period.
Pₙ is the expected selling price of the stock at the end of year N.
N is the investor’s holding period.

In this model, the investor forecasts dividends for a specific number of years (N) and then estimates the selling price of the stock at the end of that period. This helps solve the problem of infinite dividend streams by setting a realistic endpoint for the stock’s value.

Constant Growth Model (Gordon Model)

A more specialized version of the Dividend Discount Model is the Constant Growth Model, also known as the Gordon Growth Model. This model assumes that dividends will grow at a constant rate indefinitely. It’s particularly useful for valuing stable, mature companies with a long history of consistent dividend payments.

The formula for this model is:

P0=D1R−GP_0 = \frac{D_1}{R – G}

Where:

D₁ is the expected dividend at the end of year 1.
R is the required rate of return.
G is the constant growth rate of dividends.

This simplified formula is ideal for situations where dividends are expected to grow at a consistent rate, and the company’s growth prospects are stable.

Example of the Constant Growth Model

Let’s consider an example where a company has an annual dividend of $10, and dividends are expected to grow at a rate of 5% each year. The required rate of return for investors is 12%. Using the Gordon Model, we can calculate the stock’s intrinsic value as:

P0=10×(1+0.05)0.12−0.05=10.50.07=150P_0 = \frac{10 \times (1 + 0.05)}{0.12 – 0.05} = \frac{10.5}{0.07} = 150

Thus, the intrinsic value of the stock is $150.

The Zero-Growth Model

In some cases, a company may pay a fixed dividend indefinitely with no growth. This is common for preferred stocks. The formula for the Zero Growth Dividend Discount Model is simply:

P0=DRP_0 = \frac{D}{R}

Where:

D is the annual dividend.
R is the required rate of return.

Multi-Stage Dividend Discount Model

For companies that experience varying growth rates at different stages of their life cycle, the Multi-Stage Dividend Discount Model is applicable. This model breaks down dividend growth into distinct periods, typically separating high-growth years from stable growth years.

For example, a company might have a high dividend growth rate for the first 5 years, followed by a more stable, lower growth rate. The Multi-Stage model accounts for these different growth rates by applying them to the appropriate time periods.

The formula for the two-stage model is:

P0=D1(1+R)1+D2(1+R)2+⋯+DN(1+R)N+PN(1+R)NP_0 = \frac{D_1}{(1 + R)^1} + \frac{D_2}{(1 + R)^2} + \cdots + \frac{D_N}{(1 + R)^N} + \frac{P_N}{(1 + R)^N}

Where Pₙ is the price at the end of the second stage, calculated using the constant growth model.

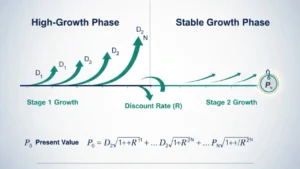
Practical Example: Using the Multi-Stage Model

Let’s assume you’re evaluating a stock that is expected to have high growth for the first 3 years, followed by lower, stable growth afterward. The dividends for the first 3 years are projected to be $2, $2.5, and $3, with a stable growth rate of 4% afterward. The required rate of return is 8%.

First, calculate the present value of the dividends during the high-growth phase, then use the constant growth model to estimate the intrinsic value beyond year 3, and discount everything back to today.

Conclusion

The Dividend Discount Model provides investors with a robust framework for determining the intrinsic value of a stock based on its future dividend payments. Whether using the basic model, constant growth model, or multi-stage model, DDM helps investors assess the long-term value of dividend-paying stocks and make informed investment decisions.

Generally, the model performs best for companies with predictable and stable dividend histories. While it’s an incredibly valuable tool, it’s important to consider the assumptions behind the model, such as constant growth or the accuracy of future dividend projections.